01851 Verfahrenssoftware für Risikomanagementsysteme
|
Die dem Beitrag zugrunde liegende Systematik für Risikomanagementsoftware unterscheidet zwischen den beiden komplementären Konzepten Systemsoftware und Verfahrenssoftware. Risikomanagementsoftware besteht aus einem Kern von Systemsoftware, der den allgemeinen Workflow und damit den Risikomanagementprozess treibt. Ein solcher Workflow bindet den Risikomanagementprozess in einen geregelten Kreis nach dem PDCA-Konzept ein.
Risikomanagementsoftware hat um diesen Kreis von Systemsoftware herum Verfahrenssoftware in Abhängigkeit von den Risiken, den Stakeholdern dieser Risiken und den einzusetzenden Verfahren angehängt.
Die Verfahren unterstützen bestimmte Teile des Risikomanagementprozesses und übernehmen die besonderen und spezifischen Aufgaben des Risikomanagements. In diesem Beitrag geht es ausschließlich um Software zur Unterstützung der Verfahren für Risikomanagementsysteme. Kommerzielle Risikomanagementsoftwareprodukte werden bewusst nicht genannt. von: |
1 Vorbemerkung zu Verfahrenssoftware
Systemsoftware für Managementsysteme unterstützt nicht nur den Workflow des Betriebs eines Managementsystems, sondern treibt und taktet ihn logisch und zeitlich. Die Systemsoftware bringt den Prozess des Managementsystems und im Falle von ISO und verwandten Standards den PDCA-Regelmechanismus für diesen Prozess in die Umsetzung. Im Beitrag „Systemsoftware für Risikomanagementsysteme” wurde dieses Konzept für Risikomanagement dargestellt (s. Kap. 01850).
Verfahrenssoftware zu Managementsystemen ist mit Systemsoftware verknüpft. Bestimmte Risiken in einem bestimmten Teilabschnitt eines Risikomanagementprozesses werden einem Verfahren unterzogen. Software unterstützt dieses Verfahren. Das Merkmal, das Verfahrenssoftware ausmacht, ist die Spezialisierung auf eine bestimmte Aufgabe in einem der Teilprozesse des Managementprozesses und des Workflows von Risikomanagement. Einige solcher Verfahren für das Risikomanagement sind zum Beispiel in der Norm DIN EN 31010 [1] beschrieben.
Verfahren, Methode, Werkzeug, Tool
Managementverfahren
Risiko wird im Prozess des Risikomanagements mehreren Verfahren unterzogen. Ein Verfahren ist die Anwendung einer Methode. Ein Werkzeug ist ein Hilfsmittel für die Anwendung. Softwareprogramme sind Werkzeug zur Unterstützung und zur Durchführung der Verfahren.
Risiko wird im Prozess des Risikomanagements mehreren Verfahren unterzogen. Ein Verfahren ist die Anwendung einer Methode. Ein Werkzeug ist ein Hilfsmittel für die Anwendung. Softwareprogramme sind Werkzeug zur Unterstützung und zur Durchführung der Verfahren.
Das Merkmal von Verfahrenssoftware ist: Die Software ist keine informationstechnische Realisierung eines vollständigen Managementsystems, oder eines vollständigen Managementprozesses oder eines vollständigen Workflows, sondern ein Teil davon.
Verfahren der Risikobeurteilung
Die Norm DIN EN 31010 dokumentiert insgesamt 31 Verfahren der Risikobeurteilung. Risikobeurteilung ist dabei ein Teilprozess des Risikomanagementprozesses nach Normkapitel 5.4, ISO 31000:2009.
Die Norm DIN EN 31010 dokumentiert insgesamt 31 Verfahren der Risikobeurteilung. Risikobeurteilung ist dabei ein Teilprozess des Risikomanagementprozesses nach Normkapitel 5.4, ISO 31000:2009.
Einige dieser Verfahren nutzen Software zur Unterstützung der Verfahren. Andere Verfahren nutzen Software zur Durchführung der Verfahren. Nicht alle dieser 31 Verfahren lassen sich auf schriftliche, grafische oder bildliche Dokumentation einer Unterstützung des Verfahrens reduzieren. Einige der Verfahren benötigen eine Durchführung des Verfahrens mit informationstechnischen Kapazitäten, insbesondere Rechenleistung und Datenspeicher, um programmierte Algorithmen ausführen zu können.
Nicht alle Verfahren für Risikomanagement geeignet
Nicht alle dieser 31 Verfahren der Norm sind nur für Risikomanagement nützlich und anwendbar. Einige der Verfahren sind im Zusammenhang mit dem Management von anderen Sachverhalten als Risiko bekannt. So ist das Verfahren FMEA (Normkapitel B.13) traditionell ein Verfahren der Beurteilung von Fehlern im operativen Qualitätsmanagement. Das Verfahren, Information in Form einer Checkliste (Normkapitel B.3) zu führen, hat originär gar nichts mit Risiko und Risikomanagement zu tun.
Nicht alle dieser 31 Verfahren der Norm sind nur für Risikomanagement nützlich und anwendbar. Einige der Verfahren sind im Zusammenhang mit dem Management von anderen Sachverhalten als Risiko bekannt. So ist das Verfahren FMEA (Normkapitel B.13) traditionell ein Verfahren der Beurteilung von Fehlern im operativen Qualitätsmanagement. Das Verfahren, Information in Form einer Checkliste (Normkapitel B.3) zu führen, hat originär gar nichts mit Risiko und Risikomanagement zu tun.
Neben diesen 31 Verfahren gibt es viele weitere Verfahren, die nicht in dieser Norm oder einer anderen Norm gelistet sind. Einige dieser Verfahren werden in diesem Beitrag ebenfalls genannt.
2 Einleitung
Information im Mittelpunkt
Software zu Risikomanagementverfahren ist Software, die Information zu Risiko und dem Management von Risiko zum Gegenstand hat. Sie ist mit der Software zum Risikomanagementsystem verknüpft und damit in den Workflow und den Prozess des Risikomanagements integriert. Informationstechnologie, insbesondere das Intranet in der Organisation und die verwendeten Programme, bildet die Infrastruktur für Risikomanagement. Information wird aus Information erzeugt (Bearbeitung), Information wird verteilt (Kommunikation) und Information wird bewahrt (Dokumentation).
Software zu Risikomanagementverfahren ist Software, die Information zu Risiko und dem Management von Risiko zum Gegenstand hat. Sie ist mit der Software zum Risikomanagementsystem verknüpft und damit in den Workflow und den Prozess des Risikomanagements integriert. Informationstechnologie, insbesondere das Intranet in der Organisation und die verwendeten Programme, bildet die Infrastruktur für Risikomanagement. Information wird aus Information erzeugt (Bearbeitung), Information wird verteilt (Kommunikation) und Information wird bewahrt (Dokumentation).
„Office”-Dokumente für Verfahren
Papier- und Bleistift-Ersatz
Nicht alle diese Verfahren benötigen zur Durchführung eine Software als Werkzeug. Viele Verfahren können grundsätzlich völlig analog „mit Papier und Bleistift” durchgeführt werden. Viele Verfahren wurden früher ohne die digitale Arbeitsstufe einer Software durchgeführt.
Nicht alle diese Verfahren benötigen zur Durchführung eine Software als Werkzeug. Viele Verfahren können grundsätzlich völlig analog „mit Papier und Bleistift” durchgeführt werden. Viele Verfahren wurden früher ohne die digitale Arbeitsstufe einer Software durchgeführt.
In der Praxis erfährt heute jedes Verfahren eine Unterstützung seiner Durchführung durch Software. Selbst eine triviale Liste von Risiken, eine Checkliste, wird als Dokument mit einer Officesoftware erstellt und in einer Dokumentenmanagementsoftware geführt. Einfachste grafische Strukturen zur Ordnung von Information, wie die einer 2×2-Matrix (z. B. die SWOT-Methodik) werden ebenfalls als Dokument mit einer Officesoftware erstellt und in einer Dokumentenmanagementsoftware geführt.
Programme für Berechnung von Algorithmen
Einige Verfahren benötigen zur Durchführung eine spezielle und individuelle Software als Werkzeug. Das trifft insbesondere für Verfahren zu, die eine statistische mathematische Grundlage haben. Statistische Risikobewertung mit Simulationen auf stochastischer Grundlage benötigen erhebliche numerische Berechnungen, die nur mit programmierten Algorithmen erfolgen können. Eine numerische Berechnung eines solchen Algorithmus ohne Software als Werkzeug nur „mit Papier und Bleistift plus Würfel als Zufallsgenerator” einer solchen Numerik mit Millionen von Rechenschritten und Millionen von Würfelschritten ist zeitlich unmöglich. Deren Ergebnisse sind Daten, die numerisch und grafisch dargestellt werden.
Manche dieser numerischen Algorithmen können mit geringem Programmieraufwand mithilfe von Officesoftware, insbesondere mit Tabellenkalkulationen, durchgeführt werden. Andere dieser Algorithmen erfordern individuelle und spezifische Software für hohe Rechengeschwindigkeit und große Datenvolumen.
Logistik von Information
Zusammengeführt werden diese IT-unterstützen und IT-durchgeführten Verfahren mit den generierten Dokumenten in einem Dokumentenmanagementsystem (Bewahrung und Verteilung von Dokumenten), das die Anforderungen der Revisionssicherheit sowie Zertifizierungs- und Testierungsunterstützung erfüllt und damit die klassische „Lenkung von Dokumenten” nach dem bekannten Konzept des Qualitätsmanagements der ISO 9001 in der alten Revision von 2008 mithilfe von Informationstechnologie ermöglicht.
Informations- bzw. Datensicherheit
Ausgehend von gesetzlichen Vorgaben und Regularien existieren standardisierte Anforderungen an Informations- und Datensicherheit, die durch weitere Spezifikationen definiert sind. Organisationen müssen Compliance zu diesen Anforderungen schaffen, indem sie nachweisen, die Standards aus den Regularien einzuhalten. Unternehmen, die ein Managementsystem zur Informationssicherheit nach der Norm ISO/IEC 27001 [2] betreiben, entsprechen diesen Anforderungen.
3 Übersicht über ausgewählte Verfahren, Software und Anwendung
Einige Beispiele zu Verfahren, die mithilfe von Software im Risikomanagement angewandt werden, finden Sie in den folgenden drei Abschnitten:
| 3.1 | Suchen und Finden von Risiken |
| 3.2 | Analysieren von Risiken und Zusammenhängen |
| 3.3 | Beurteilung (Bewertung) von Risiken |
3.1 Suchen und Finden von Risiken
Die erste Frage im Risikomanagement im Zusammenhang mit Verfahrenssoftware ist: „Was sind unsere Risiken?”
Die Antwort ist ein spezifisches und individuelles Portfolio von Risiken, die als Gegenstand des Risikomanagements festgelegt werden. Das geschieht mithilfe von Verfahren, die Suchen und Finden unterstützen.
3.1.1 SWOT-Analyse
Die klassische 2×2-Matrix
Beschreibung
SWOT ist ein Ordnungsprinzip, das Sachverhalte ordnet und in vier Kategorien entsprechend den Feldern einer 2×2-Matrix steckt. Jedes Feld nimmt Sachverhalte auf, die durch zwei Attribute gekennzeichnet sind. SWOT ist gleichermaßen ein Tabellenverfahren, in dem die Matrix einer 2×2-Tabelle entspricht.
SWOT ist ein Ordnungsprinzip, das Sachverhalte ordnet und in vier Kategorien entsprechend den Feldern einer 2×2-Matrix steckt. Jedes Feld nimmt Sachverhalte auf, die durch zwei Attribute gekennzeichnet sind. SWOT ist gleichermaßen ein Tabellenverfahren, in dem die Matrix einer 2×2-Tabelle entspricht.
Software
Zum Einsatz kommt Officesoftware zur Unterstützung der Erstellung eines strukturierten grafischen oder tabellarischen Formulars als Report zur Dokumentation im Sinne einer Aufzeichnung innerhalb des Managementsystems. Daneben gibt es auch dezidierte Apps für Tabletbetriebssysteme. Innerhalb einiger kommerzieller Risikomanagementsoftwares sind Tabellen bzw. Matrizen spezifisch für SWOT vorgegeben.
Zum Einsatz kommt Officesoftware zur Unterstützung der Erstellung eines strukturierten grafischen oder tabellarischen Formulars als Report zur Dokumentation im Sinne einer Aufzeichnung innerhalb des Managementsystems. Daneben gibt es auch dezidierte Apps für Tabletbetriebssysteme. Innerhalb einiger kommerzieller Risikomanagementsoftwares sind Tabellen bzw. Matrizen spezifisch für SWOT vorgegeben.
Anwendung
SWOT ist ein Klassiker zur Ermittlung der gegenwärtigen Ausgangssituation in Bezug auf interne Stärken und Schwächen einer Organisation und externe Bedrohungen und Begünstigungen.
SWOT ist ein Klassiker zur Ermittlung der gegenwärtigen Ausgangssituation in Bezug auf interne Stärken und Schwächen einer Organisation und externe Bedrohungen und Begünstigungen.
Beispiel
In Tabelle 1 ist beispielhaft die SWOT-Analyse eines Zulieferers für Automobilhersteller aus der Gesamtsicht des Unternehmens dargestellt.
In Tabelle 1 ist beispielhaft die SWOT-Analyse eines Zulieferers für Automobilhersteller aus der Gesamtsicht des Unternehmens dargestellt.
Tabelle 1: SWOT-Tabelle eines Automobilzulieferers, Beispiel
S (strength) | W (weakness) |
Stärken (intern: Unternehmen) | Schwächen (intern: Unternehmen) |
Produktfokus | Abhängigkeit Branche Automobil |
Marktfokus | Hochpreisprodukte |
Technologieführerschaft | Schutz „intellectual property” |
O (opportunities) | T (threats) |
Chancen (extern: Markt) | Risiken (extern: Markt) |
Ursache: Elektrifizierung (Energie) Automobil | Ursache: Preisdruck der OEMs |
Ursache: Digitalisierung (Information) Automobil | Ursache: Preisentwicklung Rohstoffe |
3.1.2 Stakeholder-Analyse
Interessen der Interessierten
Beschreibung
Die Stakeholder-Analyse ordnet einer Liste von Interessierten einer Organisation die jeweiligen Werte zu, an denen diese Stakeholder interessiert sind. Aus Gefahren und Gefährdungen für diese Werte ergeben sich Risiken, diese zukünftig zu entwickeln und zu sichern.
Die Stakeholder-Analyse ordnet einer Liste von Interessierten einer Organisation die jeweiligen Werte zu, an denen diese Stakeholder interessiert sind. Aus Gefahren und Gefährdungen für diese Werte ergeben sich Risiken, diese zukünftig zu entwickeln und zu sichern.
Software
Zum Einsatz kommt Officesoftware zur Unterstützung der Erstellung eines strukturierten textlichen Formulars als Report zur Dokumentation (Aufzeichnung). Stakeholder-Analyse ist ein Tabellenverfahren. Daneben gibt es auch dezidierte Apps für Tabletbetriebssysteme.
Zum Einsatz kommt Officesoftware zur Unterstützung der Erstellung eines strukturierten textlichen Formulars als Report zur Dokumentation (Aufzeichnung). Stakeholder-Analyse ist ein Tabellenverfahren. Daneben gibt es auch dezidierte Apps für Tabletbetriebssysteme.
Anwendung
Organisationen unterliegen vielen verschiedenen Anforderungen von vielen verschiedenen Interessierten. Stakeholder-Analyse wird eingesetzt, um herauszufinden, welche Interessierten hinter den Anforderungen stehen und welche Werte für welche Interessierten zu managen sind.
Organisationen unterliegen vielen verschiedenen Anforderungen von vielen verschiedenen Interessierten. Stakeholder-Analyse wird eingesetzt, um herauszufinden, welche Interessierten hinter den Anforderungen stehen und welche Werte für welche Interessierten zu managen sind.
Beispiel
Beispielhaft ist in Tabelle 2 die Stakeholder-Analyse eines Zulieferers für Automobilhersteller dargestellt.
Beispielhaft ist in Tabelle 2 die Stakeholder-Analyse eines Zulieferers für Automobilhersteller dargestellt.
Tabelle 2: Stakeholder-Analyse eines Automobilzulieferers, Beispiel
Stakeholder/ Interessierter | Wert (materiell/immateriell) | Gefahr, Gefährdung | Risiko (möglicher Schaden/Verlust) | |
|---|---|---|---|---|
Beispiel | Beispiel | Beispiel | Beispiel | |
1 | Kunde | Produkt | Produktfehler | Auswirkung |
2 | Eigentümer | Unternehmenswert | Strategiefehler | Wertverlust |
3 | Zulieferer | Umsatz, Profit | Bieterkampf | Auftragsverlust |
4 | Umwelt | Integrität | Katastrophe | Schaden |
5 | Management | Kompetenz, Erfolg | Führungsschwäche | Wertverlust |
6 | Mitarbeiter | Arbeitsplatz | Konjunkturschwäche | Unsicherheit |
7 | Gesellschaft | Shared Value | Ertragsschwäche | Wertverlust |
3.1.3 Prüflisten (Normkapitel B.4)
Spickzettel
Beschreibung
Eine Prüfliste bzw. eine Checkliste ist eine geordnete textliche Liste von Kriterien oder Entscheidungen oder Handlungen, die bei einer Aktivität berücksichtigt werden. Eine Checkliste ist etwas sehr Einfaches mit hohem Nutzwert.
Eine Prüfliste bzw. eine Checkliste ist eine geordnete textliche Liste von Kriterien oder Entscheidungen oder Handlungen, die bei einer Aktivität berücksichtigt werden. Eine Checkliste ist etwas sehr Einfaches mit hohem Nutzwert.
Software
Officesoftware zur Unterstützung der Erstellung einer textlichen Liste (Anweisung).
Officesoftware zur Unterstützung der Erstellung einer textlichen Liste (Anweisung).
Daneben gibt es auch dezidierte Apps für Tabletbetriebssysteme.
Anwendung
Im einfachsten Fall geht es schlicht darum, eine Folge von Dingen, die zu beachten oder die durchzuführen ist, in dokumentierter Form festzuhalten. Im Sinne der Dokumente im klassischen ISO-9001-Qualitätsmanagement kann eine Prüfliste eine Anweisung sein.
Im einfachsten Fall geht es schlicht darum, eine Folge von Dingen, die zu beachten oder die durchzuführen ist, in dokumentierter Form festzuhalten. Im Sinne der Dokumente im klassischen ISO-9001-Qualitätsmanagement kann eine Prüfliste eine Anweisung sein.
Beispiel
In Tabelle 3 sind beispielhaft die Risikoklassen und Risiken aus Sicht der Unternehmensführung eines großen Sportartikelherstellers dargestellt.
In Tabelle 3 sind beispielhaft die Risikoklassen und Risiken aus Sicht der Unternehmensführung eines großen Sportartikelherstellers dargestellt.
Tabelle 3: Checkliste eines Herstellers von Lifestyle- und Sportartikeln, Beispiel
Risikoklassen | Risiken | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
regulativ | resultierend aus mangelhafter Umsetzung von | ||||||||||||||||
Gesetzen, Verordnungen, Regularien und Auflagen zu:
| |||||||||||||||||
Verträgen/Vereinbarungen aller Art, externe Normen und Standards
| |||||||||||||||||
Interne Standards und Policies | |||||||||||||||||
strategisch | resultierend aus
| ||||||||||||||||
operativ | resultierend aus
| ||||||||||||||||
finanziell | resultierend aus
|
3.1.4 Brainstorming (Normkapitel B.1)
Kreatives Chaos
Beschreibung
Brainstorming ist eine Kreativmethode mit wenigen einfachen Regeln. Brainstorming wird protokolliert. Brainstorming wird dokumentiert. Brainstorming wird oft in Verbindung mit einem übergeordneten Verfahren (z. B.: Szenariumsanalyse, Normkapitel B.10, DIN EN 31010) durchgeführt.
Brainstorming ist eine Kreativmethode mit wenigen einfachen Regeln. Brainstorming wird protokolliert. Brainstorming wird dokumentiert. Brainstorming wird oft in Verbindung mit einem übergeordneten Verfahren (z. B.: Szenariumsanalyse, Normkapitel B.10, DIN EN 31010) durchgeführt.
Software
Officesoftware zur Unterstützung des Verfahrens durch Protokollierung des Verlaufs und Dokumentierung des Ergebnisses.
Officesoftware zur Unterstützung des Verfahrens durch Protokollierung des Verlaufs und Dokumentierung des Ergebnisses.
Mindmapsoftware zur Darstellung von logischen, zeitlichen und hierarchischen Beziehungen zwischen Themen und Sachverhalten des Brainstormings.
Anwendung
Brainstorming ist ein nützliches Verfahren, wenn es um Neues und Unbekanntes geht. Es nutzt die Fähigkeit des menschlichen Denkens, neben logischer Deduktion und Induktion die Intuition einzusetzen.
Brainstorming ist ein nützliches Verfahren, wenn es um Neues und Unbekanntes geht. Es nutzt die Fähigkeit des menschlichen Denkens, neben logischer Deduktion und Induktion die Intuition einzusetzen.
3.2 Analysieren von Risiken und Zusammenhängen
Die zweite Frage im Risikomanagement ist: „Welches sind die Zusammenhänge um ein Risiko?” Zweck dieser Frage ist, die Ursachen und die Wirkungen von Gefährdungen von Werten zu identifizieren, um die entsprechenden Risiken zu beurteilen, zu managen und zu überwachen.
3.2.1 Ursache-Wirkung-Analyse (Normkapitel B.17)
Risiko verstehen
Beschreibung
Ursache-Wirkungs-Beziehungen im Sinne von logisch kausalen Folgen (wenn → dann) und zeitlich kausalen Folgen (zuerst → danach) sind wichtig für das Erkennen von Zusammenhängen. Mehrere der in der Norm gelisteten Verfahren haben Beziehungen zwischen Ursachen und Wirkungen zum Gegenstand. Neben der Ursache-Wirkungs-Analyse gibt es verwandte Verfahren aus der Norm DIN EN 31010, die entweder auf der Seite der Ursachen oder auf der Seite der Wirkungen mit weiteren Kriterien Sachverhalte ordnen:
Ursache-Wirkungs-Beziehungen im Sinne von logisch kausalen Folgen (wenn → dann) und zeitlich kausalen Folgen (zuerst → danach) sind wichtig für das Erkennen von Zusammenhängen. Mehrere der in der Norm gelisteten Verfahren haben Beziehungen zwischen Ursachen und Wirkungen zum Gegenstand. Neben der Ursache-Wirkungs-Analyse gibt es verwandte Verfahren aus der Norm DIN EN 31010, die entweder auf der Seite der Ursachen oder auf der Seite der Wirkungen mit weiteren Kriterien Sachverhalte ordnen:
| • | Analyse der geschäftlichen Auswirkungen (Normkapitel B.11) |
| • | Ursachenanalyse (Normkapitel B.12) |
| • | Fehlerzustandsbaumanalyse (Normkapitel B.14) |
| • | Ereignisbaumanalyse (Normkapitel B.15) |
| • | Ursachen-Folgen-Analyse (Normkapitel B.16) |
| • | „Bow-Tie”-Analyse” (Normkapitel B.21) |
Die grafischen Ursache-Wirkung-Beziehungen werden in diesen weiteren Verfahren z. B. durch Baumstrukturen oder durch Fischgrätstrukturen veranschaulicht.
Wesentlich ist, dass diese Verfahren genutzt werden können, um die Normforderung nach Ermittlung von Zusammenhängen (nach ISO 31000:2009 [3] sowie Normkapitel 4 „Kontext” z. B. der ISO Normen DIN EN ISO 9001:2015 [4] und DIN EN ISO 14001:2015 [5]) zu erfüllen.
Das Verfahren kann mit dem Verfahren des Brainstormings (Normkapitel B.1) verknüpft werden.
Software
Zur Unterstützung der Erstellung einer strukturierten textlichen und grafischen Aufzeichnung und Dokumentation wird Software genutzt, die grafisch und visuell Beziehungen, insbesondere Ursache-Wirkungs-Beziehungen darstellt. Die Beziehungen sind logischer, zeitlicher oder hierarchischer Art. Die meisten der Softwarerealisierungen greifen Konzepte von Mindmap auf und bringen diese in engere Beziehungen zu Risikomanagement.
Zur Unterstützung der Erstellung einer strukturierten textlichen und grafischen Aufzeichnung und Dokumentation wird Software genutzt, die grafisch und visuell Beziehungen, insbesondere Ursache-Wirkungs-Beziehungen darstellt. Die Beziehungen sind logischer, zeitlicher oder hierarchischer Art. Die meisten der Softwarerealisierungen greifen Konzepte von Mindmap auf und bringen diese in engere Beziehungen zu Risikomanagement.
Die Ursache-Wirkungs-Analyse und die verwandtem Verfahren werden am übersichtlichsten auf grafischen Arbeitsflächen umgesetzt.
Programm
makeupmymind (experimentelle Steinbeis Software) ist eine konfigurierbare Ursache-Wirkungs-Analyse-Software nach den MindMap-Prinzip. Die Konfiguration erstreckt sich auf typische Zusammenhänge in der Praxis von Risikomanagement.
makeupmymind (experimentelle Steinbeis Software) ist eine konfigurierbare Ursache-Wirkungs-Analyse-Software nach den MindMap-Prinzip. Die Konfiguration erstreckt sich auf typische Zusammenhänge in der Praxis von Risikomanagement.
Anwendung
Die Analyse der Zusammenhänge von Ursachen und Wirkungen ist nicht nur für das Management von Risiko, sondern für das Management von allen Sachverhalten von Bedeutung. Zusammenhänge von Ursachen und Wirkungen sind z. B. im Normkapitel 4. Kontext der DIN EN ISO 9001:2015 oder DIN EN ISO 14001:2015 niedergelegt.
Die Analyse der Zusammenhänge von Ursachen und Wirkungen ist nicht nur für das Management von Risiko, sondern für das Management von allen Sachverhalten von Bedeutung. Zusammenhänge von Ursachen und Wirkungen sind z. B. im Normkapitel 4. Kontext der DIN EN ISO 9001:2015 oder DIN EN ISO 14001:2015 niedergelegt.
Beispiel
Das Beispiel in Abbildung 1 zeigt eine Arbeitsfläche mit Feldern für Einträge, die für allgemeines Risikomanagement vorkonfiguriert ist. Charakteristisch ist die logische Wirkungskette von der Ur-Ursache eines Ereignisses über das Ereignis bis zur End-Wirkung. Dazwischen liegen weitere vernetzte Ursachen und Wirkungen unmittelbarer und mittelbarer Natur in Bezug auf das Ereignis. Ergänzt wird diese Kette durch Faktoren, die Risiko verstärken oder verringern, sowie Auslöser für das eigentliche Risikoereignis.
Abb. 1: Ursache-Wirkungs-Analyse im grafischen Stil von MindMap-Verfahren
Das Beispiel in Abbildung 1 zeigt eine Arbeitsfläche mit Feldern für Einträge, die für allgemeines Risikomanagement vorkonfiguriert ist. Charakteristisch ist die logische Wirkungskette von der Ur-Ursache eines Ereignisses über das Ereignis bis zur End-Wirkung. Dazwischen liegen weitere vernetzte Ursachen und Wirkungen unmittelbarer und mittelbarer Natur in Bezug auf das Ereignis. Ergänzt wird diese Kette durch Faktoren, die Risiko verstärken oder verringern, sowie Auslöser für das eigentliche Risikoereignis.
3.3 Beurteilung (Bewertung) von Risiken (DIN EN 31010:2010)
Die dritte Frage: „Wie relevant und insbesondere wie groß ist ein Risiko?” Risiko ist als virtueller, möglicher Wert in der Zukunft zu beurteilen. Es geht um die Relevanz eines Risikos: Muss das Risiko beachtet werden? Es geht um die Größe von Risiko: Wie groß ist das Risiko in Bezug auf einen Risikomaßstab. In bestimmten Fällen muss Risiko in finanziellem Format berichtet werden, sodass Risiken in finanzieller Werteinheit gemessen werden müssen.
3.3.1 Risikoindices (Normkapitel B.28)
Risiko messen, zählen, schätzen
Beschreibung
Risikoindices sind Maßzahlen für die Relevanz von Risiken. Die Norm DIN EN 31010 beschränkt das Verständnis auf halbquantitative Größen, die es ermöglichen, die Reihenfolge von Risiken nach bestimmten Kriterien zu ermitteln.
Risikoindices sind Maßzahlen für die Relevanz von Risiken. Die Norm DIN EN 31010 beschränkt das Verständnis auf halbquantitative Größen, die es ermöglichen, die Reihenfolge von Risiken nach bestimmten Kriterien zu ermitteln.
In Erweiterung des Normverständnisses von Risikoindices als semiquantitative Größen werden in der Praxis die folgenden Praktiken für Risikoindices gepflegt.
Ordinale Zahlen (1):
Die Menge der natürlichen Zahlen 1, 2, 3, ... gibt eine Reihung an im Sinne von Platz 1, Platz 2, Platz 3. Es ist keine Metrik in diesen Ordinalzahlen definiert. Beispiel: „2” ist nicht „2*1” oder „1+1”. Es ist nur eine Reihung definiert. Ein Risiko mit dem Index 1 nimmt in einer Reihe von Risiken den 1. Platz ein.
Die Menge der natürlichen Zahlen 1, 2, 3, ... gibt eine Reihung an im Sinne von Platz 1, Platz 2, Platz 3. Es ist keine Metrik in diesen Ordinalzahlen definiert. Beispiel: „2” ist nicht „2*1” oder „1+1”. Es ist nur eine Reihung definiert. Ein Risiko mit dem Index 1 nimmt in einer Reihe von Risiken den 1. Platz ein.
Ordinale Zahlen (2):
Zusätzlich zu den Festlegungen bei den ordinalen Zahlen (1) ist hier die Metrik der Multiplikation definiert. Dies ist die Praxis bei dem Verfahren Fehlerzustandsart- und -auswirkungsanalyse – FMEA nach Normkapitel B.13 (s. Abschnitt 3.3.3). Das FMEA-Verfahren definiert einen Risikoindex für einen Fehler, die Risikoprioritätenzahl. Sie wird als Produkt dreier Indices für Fehler berechnet und kann bestimmte Werte zwischen 1 und 1000 annehmen. Sie gibt eine Priorität an in dem Sinne, dass größere Zahlen eine höhere Priorität bedeuten.
Zusätzlich zu den Festlegungen bei den ordinalen Zahlen (1) ist hier die Metrik der Multiplikation definiert. Dies ist die Praxis bei dem Verfahren Fehlerzustandsart- und -auswirkungsanalyse – FMEA nach Normkapitel B.13 (s. Abschnitt 3.3.3). Das FMEA-Verfahren definiert einen Risikoindex für einen Fehler, die Risikoprioritätenzahl. Sie wird als Produkt dreier Indices für Fehler berechnet und kann bestimmte Werte zwischen 1 und 1000 annehmen. Sie gibt eine Priorität an in dem Sinne, dass größere Zahlen eine höhere Priorität bedeuten.
Rationale Zahlen:
Die Menge der ganzen und gebrochenen Zahlen. Es sind Metriken wie die der vier Grundrechenarten definiert. In der Anwendung im Risikomanagement sind diese Zahlen vollquantitativ. Mit diesen Zahlen werden üblicherweise absolute finanzielle Werte wie auch relative Größen dargestellt.
Die Menge der ganzen und gebrochenen Zahlen. Es sind Metriken wie die der vier Grundrechenarten definiert. In der Anwendung im Risikomanagement sind diese Zahlen vollquantitativ. Mit diesen Zahlen werden üblicherweise absolute finanzielle Werte wie auch relative Größen dargestellt.
Mit den rationalen Zahlen in der Bedeutung von Geldwert, z. B. € (als Schadensausmaß in der Risikomatrix gemäß Normkapitel B.29) sind Metriken definiert. In diesem Zahlensystem sind die üblichen finanziellen Berichte formuliert. Für rationale Zahlen (z. B. für den Geldwert €) gelten die Beispiele:
3 € + 2 € = 5 €3 € – 4 € = –1 €3 € × 2 = 6 €35 € / 7 = 5 €35 € / 7 € = 57 € / 35 € = 0,2 = 20 %
Die Beispiele sind trivial.
Mit den rationalen Zahlen in der Bedeutung von Prozentwerten (% als Eintrittswahrscheinlichkeit in der Risikomatrix gemäß Normkapitel B.29) sind ebenfalls Metriken definiert. In diesem Zahlensystem sind die üblichen finanziellen Berichte formuliert. Für rationale Zeiten (z. B. für %) gelten die Beispiele:
7 € / 35 € = 0,2 = 20 %20 % + 30 % = 50 %2 × 20 % = 40 %50 % / 5 % = 10
Diese Beispiele sind trivial.
Software
Software für die Anzeige von Zahlen in numerischer Form und in grafischer Form ist definitiv nichts Besonderes. Derartige Darstellungen sind in diversen Softwarerealisierungen oft in verschiedenen Stilen frei konfigurierbar.
Software für die Anzeige von Zahlen in numerischer Form und in grafischer Form ist definitiv nichts Besonderes. Derartige Darstellungen sind in diversen Softwarerealisierungen oft in verschiedenen Stilen frei konfigurierbar.
Anwendung
Risikoanzeigen in Form von Zahlen und Grafen sind Bestandteil von Informationssystemen für Managementsysteme sowie von digitalen Berichten.
Risikoanzeigen in Form von Zahlen und Grafen sind Bestandteil von Informationssystemen für Managementsysteme sowie von digitalen Berichten.
Beispiel
Die Abbildung 2 zeigt eine Kennzahl, eine Prozentzahl, auf einem pseudo-analogen Rundinstrument (Tachometer von 0 bis 100 %) in Verbindung mit einer numerischen und digitalen Zahlenanzeige an.
Abb. 2: Cockpitanzeige einer Kennzahl (z. B.: Wahrscheinlichkeit in 0 bis 100 %) im analogen und digitalen Stil
Die Abbildung 2 zeigt eine Kennzahl, eine Prozentzahl, auf einem pseudo-analogen Rundinstrument (Tachometer von 0 bis 100 %) in Verbindung mit einer numerischen und digitalen Zahlenanzeige an.
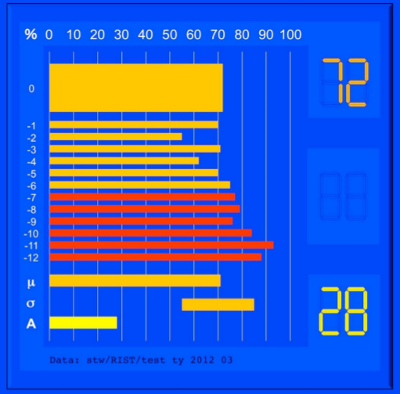
Die Abbildung 3 zeigt eine Kennzahl, deren Verlauf in den letzten zwölf Monaten sowie weitere statistische Größen mit linearen analogen Skalen (Bargraf von 0 bis 100) und einige weitere numerische und digitale Zahlenwerte an.
Abb. 3: Cockpitanzeige einer Kennzahl (z. B.: Wahrscheinlichkeit 0 bis 100 %) im analogen und digitalen Stil plus weitere Kennzahlen (Verlauf und statistische Parameter)
3.3.2 Folgen-Wahrscheinlichkeitsmatrix (Normenkapitel B.29)
Grafikikone des Risikomanagements
Beschreibung
Das Verfahren der Folgen-Wahrscheinlichkeitsmatrix ist gleichzeitig die Ikone des Risikomanagements und hat es als Grafik auf die Titelseiten von Büchern und Magazinen gebracht.
Das Verfahren der Folgen-Wahrscheinlichkeitsmatrix ist gleichzeitig die Ikone des Risikomanagements und hat es als Grafik auf die Titelseiten von Büchern und Magazinen gebracht.
Risiko wird einem zweidimensionalen Messverfahren unterzogen. Die erste Dimension ist präzise, der Wert eines Schadens oder Verlusts. Die zweite Dimension ist statistisch, die Eintrittswahrscheinlichkeit eines Schadens oder Verlusts von Wert.
Es werden die Auswirkungen eines Risikos im Sinne von Schaden an Wert und Verlust von Wert korreliert mit der Wahrscheinlichkeit des Eintretens des entsprechenden Schadens- oder Verlustereignisses.
Die Matrizen werden in einer Reihe von Varianten genutzt, die etabliert sind. Jede sogenannte Risikomanagementsoftware liefert derartige Matrizen als Report über die geführten Risiken. Die üblichen Darstellungen sind halbquantitativer Natur mit mehreren Abschnitten auf den beiden korrelierenden Koordinatenachsen.
Das Verfahren ist nahezu in allen Unternehmen und Organisationen etabliert, die ein Risikomanagement betreiben. Es findet sich beispielhaft im Risiko- und Chancenbericht einiger Aktiengesellschaften, deren Anteile im DAX gehandelt werden. In diesen Unternehmen dient die Matrix als Dokumentation der Risikosituation.
Software
Nahezu jede Risikomanagementsoftware kommerzieller und nichtkommerzieller Art hat die klassische Risikomatrix als eine Berichtsform über ein Risikoportfolio. Die hier gezeigten Beispiele in Abbildung 4 und 5 zeigen Matrizen des Programms RIST, einer experimentellen und nicht-kommerziellen Software.
Nahezu jede Risikomanagementsoftware kommerzieller und nichtkommerzieller Art hat die klassische Risikomatrix als eine Berichtsform über ein Risikoportfolio. Die hier gezeigten Beispiele in Abbildung 4 und 5 zeigen Matrizen des Programms RIST, einer experimentellen und nicht-kommerziellen Software.
Anwendung
Die scheinbare Einfachheit der Risikomatrix und ihre weite Verbreitung lassen übersehen, dass sie eine große Vereinfachung von statistischen Modellen ist und die Modelle wiederum nur eine mathematisch geschlossene Abstraktion der Wirklichkeit sind. Dennoch eignet sich die Risikomatrix hervorragend zur Visualisierung von Risiken und ihrer relativen Größe und Relevanz.
Die scheinbare Einfachheit der Risikomatrix und ihre weite Verbreitung lassen übersehen, dass sie eine große Vereinfachung von statistischen Modellen ist und die Modelle wiederum nur eine mathematisch geschlossene Abstraktion der Wirklichkeit sind. Dennoch eignet sich die Risikomatrix hervorragend zur Visualisierung von Risiken und ihrer relativen Größe und Relevanz.
Beispiel 1
Die Abbildung 4 zeigt eine halbquantitative Risikomatrix der Dimension 4×4 zur Einordnung von Risiken in 16 Felder entsprechend den Abschnitten in den Dimensionen Schadens- oder Verlustausmaß und Wahrscheinlichkeit. Die Zahlen von 1 bis 16 in den Feldern der Matrix sind ordinale Kennzahlen für die Relevanz des Risikos in dem jeweiligen Feld. Für diese ordinalen Kennzahlen ist keine Arithmetik vereinbart. Die Bedeutung ist, dass 1 die höchste Relevanz hat und 16 die geringste. Die beiden Koordinatenachsen sind nicht mit Kennzahlen belegt. Ein einzelnes Risiko in einem der 16 Felder ist durch die entsprechende Prioritätenzahl und durch die beiden halbquantitativen Attribute der entsprechenden Abschnitte auf den beiden Koordinatenachsen gekennzeichnet. Die Kennzahlen entsprechen Risikoindices (vgl. Abschnitt 3.3.1).
Abb. 4: Eine typische semiquantitative Risikomatrix (das Raster der Matrix ist leer)
Die Abbildung 4 zeigt eine halbquantitative Risikomatrix der Dimension 4×4 zur Einordnung von Risiken in 16 Felder entsprechend den Abschnitten in den Dimensionen Schadens- oder Verlustausmaß und Wahrscheinlichkeit. Die Zahlen von 1 bis 16 in den Feldern der Matrix sind ordinale Kennzahlen für die Relevanz des Risikos in dem jeweiligen Feld. Für diese ordinalen Kennzahlen ist keine Arithmetik vereinbart. Die Bedeutung ist, dass 1 die höchste Relevanz hat und 16 die geringste. Die beiden Koordinatenachsen sind nicht mit Kennzahlen belegt. Ein einzelnes Risiko in einem der 16 Felder ist durch die entsprechende Prioritätenzahl und durch die beiden halbquantitativen Attribute der entsprechenden Abschnitte auf den beiden Koordinatenachsen gekennzeichnet. Die Kennzahlen entsprechen Risikoindices (vgl. Abschnitt 3.3.1).
Beispiel 2
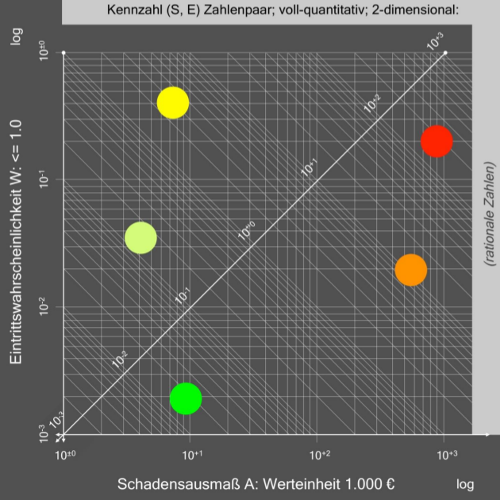
Die Abbildung 5 zeigt eine vollquantitative Risikomatrix. Die Darstellung ist doppelt logarithmisch. Die Koordinatenachsen zeigen jeweils einen Bereich über drei Größenordnungen. Die vertikale Achse zeigt einen Wahrscheinlichkeitsbereich von 0,001 bis 1,0, entsprechend 0,1 % bis 100 %. Die horizontale Achse zeigt einen Schadens- oder Verlustbereich zwischen 1 und 1.000 in der Bedeutung einer Werteinheit, wie z. B. Geldwert in 1.000 Euro. Die Zahlenskalierungen beider Achsen sind rationale Zahlen. Die Kennzahlen entsprechen Risikoindices (vgl. Abschnitt 3.3.1).
Abb. 5: Eine typische vollquantitative Risikomatrix (das Raster der Matrix ist mit einigen Datenpunkten als Beispiel gefüllt)
Die Abbildung 5 zeigt eine vollquantitative Risikomatrix. Die Darstellung ist doppelt logarithmisch. Die Koordinatenachsen zeigen jeweils einen Bereich über drei Größenordnungen. Die vertikale Achse zeigt einen Wahrscheinlichkeitsbereich von 0,001 bis 1,0, entsprechend 0,1 % bis 100 %. Die horizontale Achse zeigt einen Schadens- oder Verlustbereich zwischen 1 und 1.000 in der Bedeutung einer Werteinheit, wie z. B. Geldwert in 1.000 Euro. Die Zahlenskalierungen beider Achsen sind rationale Zahlen. Die Kennzahlen entsprechen Risikoindices (vgl. Abschnitt 3.3.1).
3.3.3 Fehlerzustandsart- und -auswirkungsanalyse (FMEA) (Normkapitel B.13)
Fehler als Nahtstelle von Risiko und Qualität
Das Verfahren FMEA ist seit vielen Jahren in vielen Varianten etabliert zur vorsorgenden Behandlung von zukünftigen Fehlern. Es wird in produzierenden Unternehmen im Rahmen des strategischen Qualitätsmanagements und der operativen Qualitätssicherung eingesetzt. Fehler werden mit drei unabhängigen natürlichen Kennzahlen bewertet. Die Kennzahlen beschreiben die drei Komponenten von Risiko in der Folge von Fehlern:
| • | Fehlerwahrscheinlichkeit ( 1 – unwahrscheinlich bis 10 – höchstwahrscheinlich) |
| • | Fehlerauswirkung ( 1 – vernachlässigbar bis 10 – äußerst groß) |
| • | Entdeckungswahrscheinlichkeit (10 – unwahrscheinlich bis 1 – höchstwahrscheinlich) |
Risikopriorität
Für diese Kennzahlen ist mit dem Verfahren FMEA die Metrik der Multiplikation definiert. Das Produkt der drei Kennzahlen liefert die Kennzahl Risikopriorität. Das Konzept dieser vorbeugenden Behandlung zukünftiger Fehler im Sinne einer Vermeidung ist in der Norm DIN EN ISO 9001 als ein Teil der Anforderung, Risikomanagement zu betreiben, aufgegriffen worden.
Für diese Kennzahlen ist mit dem Verfahren FMEA die Metrik der Multiplikation definiert. Das Produkt der drei Kennzahlen liefert die Kennzahl Risikopriorität. Das Konzept dieser vorbeugenden Behandlung zukünftiger Fehler im Sinne einer Vermeidung ist in der Norm DIN EN ISO 9001 als ein Teil der Anforderung, Risikomanagement zu betreiben, aufgegriffen worden.
Die verwendeten Risikoindices (s. Abschnitt 3.3.1) sind die ordinalen Zahlen von 1 bis 10, für die Multiplikation als Metrik definiert ist. Das Produkt, die Kennzahl Risikopriorität, kann Werte von 1 bis 1.000 annehmen. Unternehmen setzten üblicherweise ein Limit für die Risikopriorität. Fehler mit einer höheren Priorität sind zu vermeiden. Fehler mit einer geringeren Priorität können akzeptiert werden.
Die Risikomatrix nach Abschnitt 3.3.2 ist verwandt mit dem FMEA-Verfahren. Die Risikomatrix zeigt Risiko in zwei Dimensionen mit zwei Risikoindices, die FMEA zeigt Risiko in drei Dimensionen mit drei Risikoindices.
Software
Das klassische FMEA-Verfahren kann einfach mithilfe einer Tabellenkalkulation aus Officesoftware realisiert werden. Daneben gibt es dezidierte Software.
Das klassische FMEA-Verfahren kann einfach mithilfe einer Tabellenkalkulation aus Officesoftware realisiert werden. Daneben gibt es dezidierte Software.
Anwendung
FMEA wird in nahezu allen entwickelnden und produzierenden Unternehmen angewandt. Klassische Beispiele sind medizintechnische Produkte, die im Rahmen eines Qualitätsmanagements einem Produktrisikomanagement in Entwicklung, Produktion und Distribution unterzogen werden. FMEA ist das gängige Verfahren, Produktrisikomanagement zu operationalisieren. Ähnliches gilt für die Automobilindustrie mit ihren Herstellern und Zulieferern.
FMEA wird in nahezu allen entwickelnden und produzierenden Unternehmen angewandt. Klassische Beispiele sind medizintechnische Produkte, die im Rahmen eines Qualitätsmanagements einem Produktrisikomanagement in Entwicklung, Produktion und Distribution unterzogen werden. FMEA ist das gängige Verfahren, Produktrisikomanagement zu operationalisieren. Ähnliches gilt für die Automobilindustrie mit ihren Herstellern und Zulieferern.
3.3.4 Monte-Carlo-Simulation (Normkapitel B.24)
Risiko berechnen durch Simulation
Monte-Carlo-Simulation ist ein numerisches Verfahren zur Erzeugung von Zufallszahlen. Erst mit der Einbindung dieser Zufallszahlen in Algorithmen der Berechnung von Risiko wird aus der Monte-Carlo-Simulation ein Verfahren zur Berechnung von Risiko. Die weit verbreitete Fragestellung, die mit Monte-Carlo-Simulation beantwortet werden kann, ist die nach dem Gesamtrisiko, bestehend aus mehreren oder vielen Einzelrisiken.
Risikoaggregation mit stochastischer Simulation
Die Monte-Carlo-Simulation dient der Berechnung eines Gesamtrisikos aus mehreren Einzelrisiken. Monte Carlo übernimmt im übertragenen Sinn die Rolle eines Würfels, wobei ein numerischer Zufallsgenerator als Funktion innerhalb eines Programms zufällige Zahlen erzeugt. Die Zufallszahlen können zur Beschreibung der Verteilung von verschiedenen Eigenschaften einer Sache oder eines Sachverhalts genutzt werden.
Die Monte-Carlo-Simulation dient der Berechnung eines Gesamtrisikos aus mehreren Einzelrisiken. Monte Carlo übernimmt im übertragenen Sinn die Rolle eines Würfels, wobei ein numerischer Zufallsgenerator als Funktion innerhalb eines Programms zufällige Zahlen erzeugt. Die Zufallszahlen können zur Beschreibung der Verteilung von verschiedenen Eigenschaften einer Sache oder eines Sachverhalts genutzt werden.
a) Business-Prozess-Simulation (Risikoaggregation)
Beschreibung
Es wird die finanzielle Perspektive eines Geschäftsprozesses simuliert. Derartige Simulationen sind unter dem Titel Business-Prozess-Simulation bekannt. Auf der Kostenseite und auf der Ertragsseite bestehen Unsicherheiten, die zusammen wirken auf Unsicherheit des Ergebnisses. Diese Aggregation von Unsicherheiten und damit von Risiken wird simuliert.
Es wird die finanzielle Perspektive eines Geschäftsprozesses simuliert. Derartige Simulationen sind unter dem Titel Business-Prozess-Simulation bekannt. Auf der Kostenseite und auf der Ertragsseite bestehen Unsicherheiten, die zusammen wirken auf Unsicherheit des Ergebnisses. Diese Aggregation von Unsicherheiten und damit von Risiken wird simuliert.
Software
Risiken sind nicht einfach miteinander zu addieren oder voneinander zu subtrahieren. Ein Risiko kann nicht durch ein anderes Risiko kompensiert werden. Allenfalls kann ein Risiko durch eine Chance aufgewogen werden. Risiken in ihrer Gesamtheit werden durch Addition der Verteilung ihrer Wirkung berechnet. Diese Berechnungen erfolgen durch Simulationen.
Risiken sind nicht einfach miteinander zu addieren oder voneinander zu subtrahieren. Ein Risiko kann nicht durch ein anderes Risiko kompensiert werden. Allenfalls kann ein Risiko durch eine Chance aufgewogen werden. Risiken in ihrer Gesamtheit werden durch Addition der Verteilung ihrer Wirkung berechnet. Diese Berechnungen erfolgen durch Simulationen.
Beschreibung: Anforderungen, Aufbau, Anwendung, Nutzen, Grenzen
Für die experimentelle Software RIST sind in Excel Algorithmen geschrieben. Die Rechenzeiten auf einem PC sind für ein derart einfaches Modell unbedeutend und liegen im Bereich von Millisekunden.
Anwendung
Die Simulation bezieht sich auf das Risiko des Ergebnisses beim Einkauf (en gros) und Verkauf (en detail) zu Marktpreisen, die variieren. Für die Variation wird eine Gauss-Verteilung angenommen. Die Gauss-Verteilung ist ein Modell als Näherung der Realität. Der Business-Prozess Verkauf und Einkauf wird simuliert.
Die Simulation bezieht sich auf das Risiko des Ergebnisses beim Einkauf (en gros) und Verkauf (en detail) zu Marktpreisen, die variieren. Für die Variation wird eine Gauss-Verteilung angenommen. Die Gauss-Verteilung ist ein Modell als Näherung der Realität. Der Business-Prozess Verkauf und Einkauf wird simuliert.
Es wird das Ergebnis des Business-Prozesses als Differenz zwischen Verkaufspreis und Einkaufspreis berechnet. Verkaufspreis und Einkaufspreis sind mit einer Abweichung um einen mittleren Wert belegt. Im Algorithmus wird die Verteilung der Abweichungen durch Gauss-verteilte Zufallszahlen berücksichtig. Die Differenz wird für Tausende von Zahlenwerten für Verkaufspreis und Einkaufspreis berechnet. Die Ergebnisse werden grafisch dargestellt. Risiken aus dem Einkauf und dem Verkauf werden aggregiert.
Es wird die Monte-Carlo-Simulation der Folge von Preisschwankungen auf dem Einkaufs- und dem Verkaufsmarkt gezeigt. Das Ergebnis ist verteilt. Die verwendeten Verteilungen für dieses Demonstrationsmodell sind Gauss-Verteilungen verschiedener Standardabweichungen. Die Standardabweichung ist ein Maß für Risiko. Die Gauss-Verteilung ist umso breiter, je größer die Standardabweichung. Je größer die Standardabweichung, desto größer ist das Risiko, ein Ergebnis zu erreichen, das von einen geplanten Ziel abweicht.
| • | Verkaufspreis (VK)/en detail Marktpreise Verkaufsmarkt (blaue gestrichelte Kurve mit Maximum rechts): Gauss-Verteilung mit vorgegebener Standardabweichung; vorgegebener Mittelwert 21 € |
| • | Einkaufspreis (EK)/en gros Marktpreise Einkaufsmarkt (rote gepunktete Kurve mit Maximum Mitte): Gauss-Verteilung mit vorgegebener Standardabweichung; vorgegebener Mittelwert 15 € |
| • | Ergebnis (P/L)/Verkaufspreis (VK) – Einkaufspreis (EK) (gelbe Kurve mit Maximum links): berechnete Verteilung aus der Monte-Carlo-Simulation; simulierter Mittelwert 6 €. |
Varianten
Es können weitere variable und unsichere Kosten in die Simulation eingerechnet werden.
Es können weitere variable und unsichere Kosten in die Simulation eingerechnet werden.
Kritischer Punkt
Das Ergebnis wird stark von den verwendeten Verteilungsfunktionen beeinflusst. Die Verteilungsfunktionen können aus Vergangenheitsdaten experimentell ermittelt werden. Eine Gauss-Verteilung ist eine Näherung der Realität. Es zeigt sich das bekannte Phänomen von Programmen: Der Output ist nur so gut wie der Input.
Das Ergebnis wird stark von den verwendeten Verteilungsfunktionen beeinflusst. Die Verteilungsfunktionen können aus Vergangenheitsdaten experimentell ermittelt werden. Eine Gauss-Verteilung ist eine Näherung der Realität. Es zeigt sich das bekannte Phänomen von Programmen: Der Output ist nur so gut wie der Input.
Leistung
Transparenz über die Beiträge einzelner Kosten- und Ertragskomponenten und ihrer Risiken zum Ergebnis und zum Risiko in Verbindung mit dem Ergebnis.
Transparenz über die Beiträge einzelner Kosten- und Ertragskomponenten und ihrer Risiken zum Ergebnis und zum Risiko in Verbindung mit dem Ergebnis.
Bereiche
Das Verfahren wird angewendet z. B. bei Wiederverkäufern von Produkten und Diensten mit variablen Marktpreisen auf der Einkaufs- und der Verkaufsseite.
Das Verfahren wird angewendet z. B. bei Wiederverkäufern von Produkten und Diensten mit variablen Marktpreisen auf der Einkaufs- und der Verkaufsseite.
b) Projektdauer Simulation (Risikoaggregation)
Beschreibung
Es wird die zeitliche Perspektive eines Projekts simuliert. Einzelne Teilprojekte sind mit Risiken betreffend ihrer jeweiligen Zeitdauer belegt. Die Aggregation von Unsicherheiten und damit von Risiken wird simuliert.
Es wird die zeitliche Perspektive eines Projekts simuliert. Einzelne Teilprojekte sind mit Risiken betreffend ihrer jeweiligen Zeitdauer belegt. Die Aggregation von Unsicherheiten und damit von Risiken wird simuliert.
Ermittlung zeit- oder kostenkritischer und damit risikobehafteter Teilprojekte in einem Gesamtprojekt. Ermittlung der Zeit- und Kostensicherheit eines Projekts.
Software
Das Verfahren generiert mit Monte Carlo Zufallszahlen für die Verteilungen der Zeitdauern der Teilprojekte und berechnet daraus die Verteilung der Zeitdauer des Gesamtprojekts. Es werden die Ungewissheiten der Zeitdauern der einzelnen Projekte zu einer Ungewissheit der Zeitdauer des Gesamtprojekts aggregiert. Es ist ein Verfahren der Risikoaggregation. Der schwierige Teil des Algorithmus ist der, dass Teilprojekte entweder parallel (nebeneinander) oder seriell (hintereinander) ablaufen können. Risiken aus den Einzelprojekten werden zu einem Risiko des Gesamtprojekts aggregiert.
Das Verfahren generiert mit Monte Carlo Zufallszahlen für die Verteilungen der Zeitdauern der Teilprojekte und berechnet daraus die Verteilung der Zeitdauer des Gesamtprojekts. Es werden die Ungewissheiten der Zeitdauern der einzelnen Projekte zu einer Ungewissheit der Zeitdauer des Gesamtprojekts aggregiert. Es ist ein Verfahren der Risikoaggregation. Der schwierige Teil des Algorithmus ist der, dass Teilprojekte entweder parallel (nebeneinander) oder seriell (hintereinander) ablaufen können. Risiken aus den Einzelprojekten werden zu einem Risiko des Gesamtprojekts aggregiert.
Programm
Die experimentelle Software RIST ist für diese Anwendung in dem Programmentwicklungssystem Matlab® (The MathWorks) geschrieben. Die Rechenzeiten auf einem PC können für Projekte mit vielen Teilprojekten beträchtlich (im Bereich von Stunden) sein. Eingaben sind mögliche „Von-bis”-Zeitdauern für Teilprojekte sowie jeweils eine Annahme über die Verteilung der Zeitdauern der Teilprojekte. Ausgabe ist eine simulierte Zeitdauer für das Gesamtprojekt.
Die experimentelle Software RIST ist für diese Anwendung in dem Programmentwicklungssystem Matlab® (The MathWorks) geschrieben. Die Rechenzeiten auf einem PC können für Projekte mit vielen Teilprojekten beträchtlich (im Bereich von Stunden) sein. Eingaben sind mögliche „Von-bis”-Zeitdauern für Teilprojekte sowie jeweils eine Annahme über die Verteilung der Zeitdauern der Teilprojekte. Ausgabe ist eine simulierte Zeitdauer für das Gesamtprojekt.
Anwendung
Bei Projekten sind die drei wichtigsten Fragen:
Bei Projekten sind die drei wichtigsten Fragen:
| • | Wann ist der Fertigstellungstermin des Gewerkes mit welcher Wahrscheinlichkeit? |
| • | Was sind die Gesamtkosten des Gewerkes mit welcher Wahrscheinlichkeit? |
| • | Was ist die Leistung des Gewerkes mit welcher Wahrscheinlichkeit? |
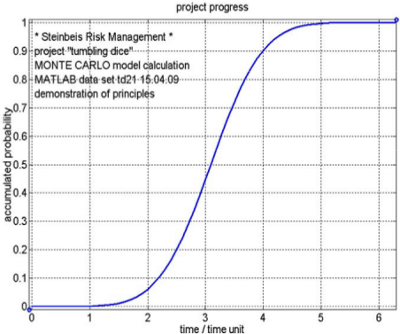
| • | Projektdauer ist 32 Monate mit 50 % simulierter Sicherheit. |
| • | Projektdauer ist 40 Monate mit 90 % simulierter Sicherheit. |
Varianten
Es kann nicht nur das Zeitrisiko (Wie lange dauert das Projekt bei z. B. 90 %iger Sicherheit in Bezug auf die Zeit?) sondern auch das Kostenrisiko (Was kostet das Projekt bei z. B. 75 %iger Sicherheit in Bezug auf die Kosten?) ermittelt werden.
Es kann nicht nur das Zeitrisiko (Wie lange dauert das Projekt bei z. B. 90 %iger Sicherheit in Bezug auf die Zeit?) sondern auch das Kostenrisiko (Was kostet das Projekt bei z. B. 75 %iger Sicherheit in Bezug auf die Kosten?) ermittelt werden.
Kritischer Punkt
Die Annahme der Verteilung der Zeitdauern der einzelnen Teilprojekte ist entscheidend für das Ergebnis.
Die Annahme der Verteilung der Zeitdauern der einzelnen Teilprojekte ist entscheidend für das Ergebnis.
Leistung
Neben der Ermittlung der Gesamtzeit werden einzelne zeitkritische Teilprojekte identifiziert und verstanden.
Neben der Ermittlung der Gesamtzeit werden einzelne zeitkritische Teilprojekte identifiziert und verstanden.
Bereiche
Das Verfahren kann grundsätzlich für jedes Projektmanagement angewandt werden.
Abb. 7: Modellierung der Zeitdauer einer Projektfertigstellung mit Monte-Carlo-Simulation
Das Verfahren kann grundsätzlich für jedes Projektmanagement angewandt werden.
3.3.5 Statistische Methoden
Operative Auswertung
Beschreibung
Statistische Methoden zur Quantifizierung von Risiken und Fehlerhäufigkeiten innerhalb des operativen Geschäfts werden im Rahmen von operativen Methoden, wie der Gefährdungsanalyse mit Kontrollen an kritischen Stellen, HACCP (vgl. Normkapitel B.7, DIN EN 31010) oder eines vergleichbaren internen Kontrollsystems durchgeführt.
Statistische Methoden zur Quantifizierung von Risiken und Fehlerhäufigkeiten innerhalb des operativen Geschäfts werden im Rahmen von operativen Methoden, wie der Gefährdungsanalyse mit Kontrollen an kritischen Stellen, HACCP (vgl. Normkapitel B.7, DIN EN 31010) oder eines vergleichbaren internen Kontrollsystems durchgeführt.
Simulation von Messungen mit standardisierten Modellen sind Messungen von Ungewissheit und Risiko. Eine Gauss-Verteilung ist letzten Endes ein Maßstab zum Messen von zwei Parametern:
| • | dem Mittelwert einer Verteilung, |
| • | der Breite einer Verteilung. |
Software
Software zur Messung von Risiko mit statistischen Modellen als Maßstab ist Bestandteil von vielen statistischen Softwarepaketen.
Software zur Messung von Risiko mit statistischen Modellen als Maßstab ist Bestandteil von vielen statistischen Softwarepaketen.
Programm
Die experimentelle Software RIST ist für diese Anwendung in dem Programmentwicklungssystem Matlab® (The MathWorks) geschrieben.
Die experimentelle Software RIST ist für diese Anwendung in dem Programmentwicklungssystem Matlab® (The MathWorks) geschrieben.
Anwendung
Das Verfahren wird auf einem laufenden Workflow eines technischen Prozesses in seiner Infrastruktur angewendet und misst an bekannten und identifizierten Stellen physikalische oder chemische Parameter, deren Verteilung an Standards angepasst wird.
Das Verfahren wird auf einem laufenden Workflow eines technischen Prozesses in seiner Infrastruktur angewendet und misst an bekannten und identifizierten Stellen physikalische oder chemische Parameter, deren Verteilung an Standards angepasst wird.
Beispiel
Eine Reihe von Messungen eines Parameters in einem technischen Prozess zeigt üblicherweise eine Verteilung. Unter bestimmten Annahmen kann diese Verteilung mit einem numerischen Verfahren an eine Gauss-Verteilung als Modell angepasst werden. Die Breite der Verteilung ist ein Maß für die Ungewissheit und damit für Risiko.
Eine Reihe von Messungen eines Parameters in einem technischen Prozess zeigt üblicherweise eine Verteilung. Unter bestimmten Annahmen kann diese Verteilung mit einem numerischen Verfahren an eine Gauss-Verteilung als Modell angepasst werden. Die Breite der Verteilung ist ein Maß für die Ungewissheit und damit für Risiko.
Die Abbildung 8 zeigt einige exemplarische und gemessene Daten eines Prozesses und eine dazu simulierte Gauss-Verteilung.
Abb. 8: Anpassung einer Gauss-Verteilung (Modell) an eine Verteilung von Messdaten (Wirklichkeit)Quellen
1
DIN EN 31010:2010, Risikomanagement – Verfahren zur Risikobeurteilung (ISO/IEC 31010:2009)
2
ISO/IEC 27001:2015, Informationstechnik – IT-Sicherheitsverfahren – Informationssicherheits-Managementsysteme – Anforderungen
3
ISO 31000:2009, Risikomanagement – Allgemeine Anleitung zu den Grundsätzen und zur Implementierung eines Risikomanagements
4
DIN EN ISO 9001:2015, Qualitätsmanagementsysteme – Anforderungen
5
DIN EN ISO 14001:2015, Umweltmanagementsysteme – Anforderungen mit Anleitung zur Anwendung
6
DIN EN 62198:2014; VDE 0050-6:2014, Risikomanagement für Projekte – Anwendungsleitfaden
7
Meier, Peter: Risikomanagement in Großprojekten/Risk Management in Mega Projects; Chemie Ingenieur Technik; Vol. 84, No. 5, 727–729; Wiley-VCH Verlag, 2012